Ole Amble'ın tezine ulaştıktan sonra şu sonuçlar çıktı: Tarihi bilgilerimize göre Ole Amble, "A Set of Formulas for Numerical Integration" adlı tezinin yayını için Prof. Sigmund Selberg'e verdi. O, 10 Mart 1952 tarihli ortak toplantıda tezin sunumunu yaptı. O da tezin yayını için komisyona teslim etti ve komisyon başkanı F. Bruns Bokhandel tarafından onaylandıktan sonra 5 Mayıs 1952'de Tröndheim'daki Aktietrykkeriet'te basılarak DKNVS'nin Cilt: XXV ve Nr: 10 no'lu sayısında yayınlandı.
Ole Amble'ın Tezinin Peşinde!
İster inanın ister inanmayın bu tezi Romberg'in tezinden beri arıyordum. Çünkü Romberg, kendi tezinde Ole Amble'ın metodu için [2] no'lu kaynakçayı işaret ediyordu ve bu tez elimde olmadan, yalnızca Romberg'in tezinden hareketle Ole Amble'ın T2 ve T3 yaklaşıklıklarını form olarak genelleştirdim (ki bunu daha iyi yakınsaklık için yapmıştım) ve T2 ve T3 ile T0 ve T1 yaklaşıklık çiftleri ve bunların ekstrapolasyonları arasındaki bağıntıları ilk kez ortaya koymuştum (Bkz. "Genelleştirilmiş Ole Amble Algoritması"). Fakat ne zaman ki C'deki Piobert-Parmentier Metodu'nu ortaya koydum (ki Ole Amble'ın metodu 19. yy.'dan kalma bu metoda dayanır), işte o zaman Ole Amble'ın tezi benim için bir ihtiyaç haline gelmişti (Bkz. "Genelleştirilmiş Piobert-Parmentier Metodu"). Böylece Ole Amble Metodu'nu anlayabilmem, dolayısıyla Piobert-Parmentier Metodu'nu tam olarak çıkartabilmem mümkün olacaktı. Ama Romberg'in işaret ettiği [2] no'lu kaynak olan Ole Amble'ın tezini NTNU'dan almam kolay olmadı. Çünkü Owren ile yazışmalarıma göre, kendisi bana ilkin bu tezin elinde olmadığını ve 03.10.2021, 04:48'de ikinci kez rahatsız ettiğimde ise elektronik olarak değil ama basılı olarak mevcut olduğunu söylemişti. Bu nedenle beni ilgili birimlere yönlendirdi. Şu tesadüfe bakın ki Norveç'in 9 Nisan 1940'taki işgalinden tam 81,5 yıl sonra Owren'in yönlendirdiği Kristian Overskaug'a 09.10.2021, 04:14'te, Sven Ström'e 04:15'te ve Magne Brekke Rabben'e 04:17'de birer e-posta yollayarak Ole Amble'ın tezini istedim (Bkz. "81 year anniversary for the German invasion of Norway-Remembering the fallen", "Norwegian fortress from world war 2. Indre Østfold Norway", "Det tyske angrepet på Oslo 1940 (1940'ta Oslo'ya Alman Saldırısı)"). Tezi NTNU'dan Sven Ström, 11.10.2021, 15:28'de (ki PDF'de oluşturma tarihi 11.10.2021, 15:19:45'tir) bana gönderdi ve ilk gözlemlerimi sıcağı sıcağına "Nihayet Ole Amble''ın tezini bulduk!" sayfasında dile getirdim!
Fakat Ole Amble'ın tezini incelerken T2, T3, T4, T5, T6, T7, T8 ve T9 yaklaşıklıklarının nasıl elde edildiğine ilişkin açık bir bilgi bulamadım. Çünkü o, bu yaklaşıklıklar için sadece sonuçlar yani formüller veriyordu ve bu sonuçları yeniden çıkarabilmek demek, o dönemki bilgileri bilmek demekti. Bu ne demek biliyor musunuz?
Danimarka'nın Cesur Evlatları
Naziler 9 Nisan 1940'ta Danimarka'nın güney sınırından içeri girdiklerinde ne olduğunu açıklamak gibi berbat bir şey bu! Veteranlar, "9 Nisan" filminin bitiminden sonra kendi ağızlarıyla Norveç'in güney sınırında neler yaşandığını anlatırlar. Buna göre o sonuçları çıkarabilmek adeta Ole Amble'ın yanında olmak gibi bir şeydi. Ama madem durum böyle, o zaman ben de Theo Findahl gibi çalışkanlığımı ortaya koyayım, dedim (Y.N. İtiraf ediniz: Theo Findahl ile Ole Amble'ın şapkaları, birbirlerini ele veriyor. Norveçli muhabir olarak adlandırılan Theodor (Theo) Findahl, evde oturup basın bültenlerini okumadı; öğretmenliğinde geçirdiği tatillerde de çalıştı: Gezi yazıları, haberler, raporlar, denemeler yazdı ve röportajlar yaptı. 1939'da Aftenposten'ın (Akşam Postası) Berlin muhabiri olarak tam zamanlı çalışmaya başladıktan sonra Sovyetler Birliği ve Amerika Birleşik Devletleri'nden kitaplar yazdı. II. Dünya Savaşı'nın başlangıcını orkestra koltuğundan izleyebildi. Diğer yabancı gazeteciler gibi o da haber muhabirliği konusunda katı kısıtlamalara tabiydi, ancak yine de ne olacağına dair ipuçları içeren bir dizi mesajla yazı işleri ofisini arayabiliyordu. 5 Nisan 1940'ta, 40,000 Alman askerinin Baltık kıyılarında toplandığına ve muhtemelen hedef olarak güney Norveç limanına sahip olduklarına dair "bir söylentiye" atıfta bulundu. Bir mesajını telefonla şöyle iletmişti: "Geliyorlar! En kısa zamanda bize bildirin". 7 Nisan'da da Aftenposten'e Almanların Norveç'e saldırısının sürmekte olduğunu telgrafla bildirdi. Gazetenin editörü mesajı komutan Amiral'e gösterdi, o da buna inanmadı ve bu nedenle yayınlamayı bıraktı).
Ole Amble'ın Tezi
Öncelikle Ole Amble'ın Romberg'ten daha ketum olduğunu belirtmem gerekiyor. Çünkü Ole Amble yukarıda anılan yaklaşıklıkların nasıl bulunduğuna ilişkin açık bir kapı bırakmamıştı, dolayısıyla ben de bu yaklaşıklıkları doğrudan bulmak yerine (4.3)'teki
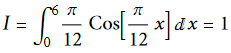
örneğinden hareketle örneğinden hareketle Ole Amble'ın elde ettiği sonuçları yakalamaya çalışarak dolaylı bir yolu tercih ettim. Bunun için ilkin (4.4)'teki A1'in 1. türev için verilen merkezi fark formülünden geldiğini biliyordum ve bu yüzden trapezli yaklaşıklıklar için diğerlerinin de merkezi fark formüllerinden gelmiş olabileceğinden hareketle "Merkezi Fark Formülleri"ndeki türev formüllerini C'de yani kompleks sayılar kümesi üzerindeki "Genelleştirilmiş Piobert-Parmentier Metodu"nda yaptığım gibi teker teker buldum ve bunları 20.10.2021, 06:45:20'de yukarıdaki örneğe uyguladığımda Ole Amble'ın sonuçlarını elde ettim (Bkz. Tablo 4.1). Bunlar trapezli yaklaşıklıklar idi ama aynı merkezi fark formüllerini orta noktalı yaklaşıklıklar için uyguladığım zaman (4.43)'ten görüldüğü üzere son 2 katsayıda hata yapılmış olduğunu gördüm. Bu nedenle uzun bir süredir "acaba ben mi hata yapıyorum yoksa Ole Amble, başka bir yöntem mi kullandı?" diye kendime gelemedim. Çünkü o sırada Ole Amble'ın kullandığı yöntemi bilmiyordum! Ancak Tablo 4.1'in son sütunundaki Ole Amble'ın sonuçları daha orta nokta formülünde göçüyordu ama 22.10.2021, 05:07:46'da bulduğum sonuçların doğru olduğuna inanıyordum. Tabii ki çok sonra "Piobert-Parmentier Metodu'nun Q Üzerinde Genelleştirilmesi" adlı tezimin nerdeyse bitime yakın Ole Amble'ın yöntemini, daha doğrusu Not 4.1'de söylediğim gibi Merkezi Fark Formülleri İçin Ole Amble'ın Formülasyonu'nu 27.11.2021, 23.11.35'te keşfettim ve böylece orta noktalı yaklaşıklıkları da doğru bir şekilde keşfettiğimi öğrendim. Aslında buna gerek yoktu ama yine de kimsenin kafasında herhangi bir soru işareti kalmasın diye Ole Amble'ın formülasyonunu çıkarttım. Daha sonra Ole Amble'ın yaklaşıklıklarına 2. Tür E-ATA Algoritması'nı uygulayarak özel bir Mathematica programı yazdım. Tüm bu gelişmeleri "Ole Amble'ın Metodu-1952" programında bulabilirsiniz!

