- +228 872 7355
-
Bu e-Posta adresi istenmeyen posta engelleyicileri tarafından korunuyor. Görüntülemek için JavaScript etkinleştirilmelidir.





-

Romberg İntegral Yöntemi'ne ilişkin bu ilk çalışmamda, daha doğrusu karalamamda şu çalışmaları yapmıştım:
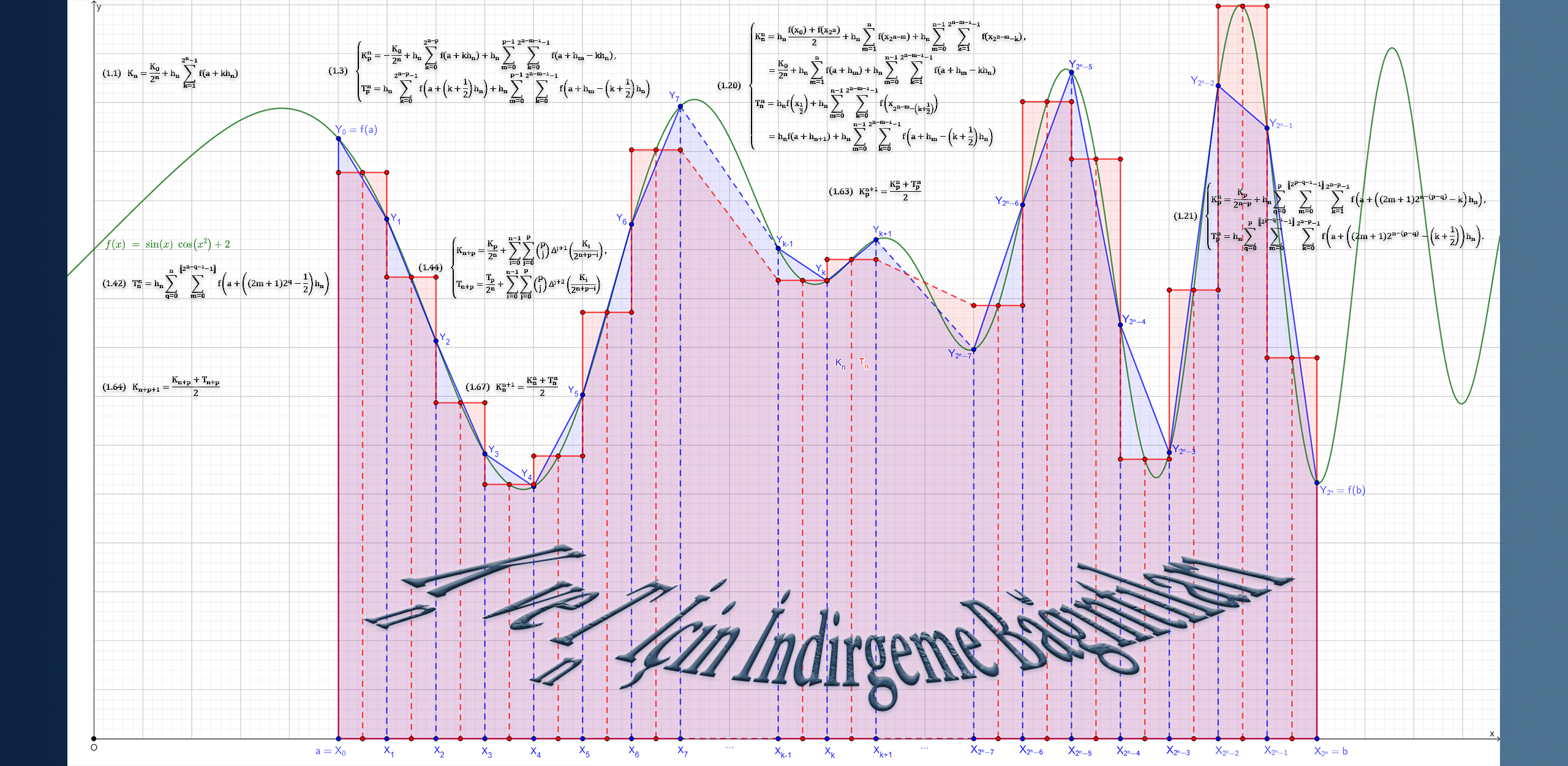
1. Romberg Metodu ve Ötesi
1.1. Trapez Metodu
1.2. Romberg Metodu'na İlikin Orijinal Formüller
1.3. An ve Bn Dizilerinin A0 ve B0 Başlangıç Terimlerine İndirgenmesi
1.4. Romberg İle Çakışmamız
1.5. Romberg'in Orijinal Makalesinin Peşinde (Not. Bu parça orijinalde yoktur; sadece durum değerlendirmesi nedeniyle ekledim)
2. Romberg Algoritmasını Richardson Dışkestirimi İle Hızlandırılması ve Ötesindeki Gelişmeler Hakkında
2.1. Richardson Dışkestirimi Alt ve Üst Sınırlarla Birlikte Çalışmaz! (Not. Bu durum Richardson dışkestiriminin Snellius algoritması formunda yazıldığı zaman ortaya çıktı)
2.2. Richardson Dışkestiriminde Aritmetik Ortalama
2.3. Tekrar Hoş Geldin Snell Amca!
2.4. Snellius-Huygens Algoritmaları Arasındaki İlişki
Adı üstünde, bu bir karalama olduğu için orijinal dosyayı olduğu gibi vermemin bir anlamı yoktu. Ben, sadece önem arz eden çalışmaları alıntılarak ve onlar hakkında açıklamalar yaparak dikkatinize sunuyorum: Romberg Metodu.
Fakat bu ilk dosya hakkında şunu açıkça söyleyebilirim ki, birkaç karalamadan ibaret olan dosyanın bu hali bile Romberg Metodu hakkında ufuk açıcı özelliklere sahiptir.
Bu arada, dosyanın Word'ten aldığım dikkat çeken belli başlı bazı özellikleri şunlardır:
Dosya Adı: Romberg Metodu
İçerik Oluşturma Tarihi: 02.11.2016, 22:44 (Not. Dosyayı 22:44'te açtım ama yazıma 22:54'te başladım. Yani çalışmanın başlangıç tarihi, 02.11.2016, 22:54'tür)
Toplam Düzenleme Süresi: 26:59:00
Düzeltme Numarası: 401
Sayfa: 16
Format: A4
Boyut: 850 KB
Burada dikkat edilirse 1 günlük 3 saat bir çalışma sözkonusudur ve bunun çoğu 2. Bölüm'deki araştırmalarda geçti. Herhalde Hollandalılar Snellius algoritmasını ekstrapolasyona kazandırdığım ve Snellius-Huygens algoritmaları arasındaki ilişkiyi gösterdiğim için çok mutlu olmuşlardır!
-

Karaoğlan BÜLENT ECEVİT'i 13. Ölüm Yıldönümünde Anıyoruz!
Öncelikle Cumhuriyetimizin ilk kuşağından, dolayısıyla Ulusalcı Lider olan Karaoğlan BÜLENT ECEVİT'i 13. ölüm yıldönümünde sevgi, saygı ve büyük bir özlemle anıyoruz!
Tesadüf bu ya, Romberg İntegrali Kronolojim 2 çalışmamda gerek Romberg'in solcu yanılsamaları nedeniyle gerekse "Adam Olmak (IF)" adlı şiiri nedeniyle ikide bir Ecevit'i anıyordum ve bu makaleyi onun ölüm yıldönümüne yetiştirdiğim için kendimi şanslı sayıyorum!
Sözkonusu bu ikinci çalışmamın içeriği şöyledir:
1. Trapez Metodu.
1.1. Trapez Metodunun Geometrik Yorumu.
1.1.1. K ve T'nin Eğimlerinin Aynı Olması Şartı.
1.1.2. Tn'nin Değişmezliği Hakkında.
1.1.3. Metodun En Etkin Şekilde Kullanılması Hakkında.
1.1.4. Kn ve Tn Arasındaki İlişki: Aritmetik Ortalama.
1.2. Romberg Metodu'na Ait Orijinal Formüller.
1.2.1. Notasyon Sorunu.
1.3. Kn'nin K0'a İndirgenmesi.
1.4. Romberg İle Çakışmamız.
2. Romberg Algoritmasının Richardson Ekstrapolasyonu İle Hızlandırılması ve Ötesindeki Gelişmeler Hakkında.
2.1. E-ATA 1 Algoritmaları.
2.1.1. Hoş Geldin Snell Amca!
2.1.1.1. Eutokios'un Kesirleri Kurgu muydu?
2.1.2. Ekstrapolasyonda Aritmetik Ortalama.
2.1.2.1. Tekrar Hoş Geldin Snell Amca!
2.1.2.1.1. Snellius-Huygens Algoritmaları Arasındaki İlişki.
Buna göre, bu 2. çalışmamda ilkine göre artık alıntılar değil, açık açık olarak yaptığım çalışmalar mevcuttur. Bu nedenle bundaki Bölüm 1 daha yetkindir. Yani bu çalışmada esas odaklandığım yer, Bölüm 1'dir. Bölüm 2 ise ilkiyle hemen hemen aynı olup, sadece Arşimet'in Önerme 3'ünü yorumlayan Eutokios'un kesirlerini Snellius algoritmasıyla inceleme farkı vardır. Orada beni şaşırtan şey, Tablo 2.3'ün son satırında geçen Van Ceulen ve Snellius'un 230-genlerle yaptıkları hesabın Arşimet'in 6, 12, 24, 48 ve 96-genleri için S0(4) ile yapılabilindiğidir (ki S0(4), Tablo 2.1'deki 5. algoritmadır).
Bunlarla birlikte Romberg İntegrali'ne ilişkin ilkinden farklı olarak orijinal ve tam olarak verdiğim bu 2. çalışmamın künyesi şöyledir (ki ilkini özet olarak vermiştim ve bu da sansürsüz olarak onun devamıdır):
Dosya Adı: Romberg Metodu.
İçerik Oluşturma Tarihi: 02.11.2016, 22:44.
Son Kaydetme Tarihi: 02.01.2017, 16:54.
Toplam Düzenleme Süresi: 42:26:00.
Düzeltme Numarası: 554.
Sayfa: 19.
Boyut 877 KB.
Format: A4.
-

Nazi Almanyası'ndan Kaçan Matematikçiler: Kaderleri ve Küresel Etkileri
Evet, büyük gün geldi çattı. Yani "Werner Romberg Türkiye'de" adlı makalemde durumu açıklamıştım. Hemen bir özet geçmem gerekirse, Atatürk'ün 1933'teki Üniversiteler Reformu sırasında Nazi Almanyası'ndan kaçan bilim adamları Türkiye'ye gelir. Bu, Atatürk için eşi bulunmaz bir fırsattır ve hemen akademisyenlerin müracaatlarını kabul eder. Buraya dikkat: Almanya'da istenmeyen Musevi akademisyenleri sadece Türkiye kabul ediyor. Çünkü diğer ülkeler Hitler korkusu yüzünden reddediyor. Amerika bile (Bkz. "Atatürk dünyanın korktuğu Hitler'e nasıl meydan okudu?"). Fakat 1 yıl sonra aklı başına gelen Hitler, Atatürk'ten Yahudi bilim adamlarını geri istiyor. Diyor ki, "Gönderin onları bana, ben size daha iyisini göndereceğim!". Tabii ki Türk Hükümeti göndermiyor, ama Hitler son ana kadar uğraşıyor. Hatta 1940'larda Gestapo'yu gönderiyor. Onlar da aynı istekte bulunuyor: "Onları gönderin!". Ancak Türk Hükümeti bunlara da dayanıyor ve yine göndermiyor (Bkz. "Hitler istedi ama Atatürk Yahudi profesörleri vermedi").
Almanya'dan kaçan bilim adamlarından bir kısmıyla Zürih'te "Yurtdışındaki Alman Bilim Adamları Yardım Cemiyeti" adlı bir dernek kurulur ve başına Philip Schwartz getirilir. Schwartz'ın teklifiyle Göttingen Üniversitesi'nden matematikçi Richard Courant, matematikçi ve fizikçi Max Born (Nobel ödüllü) ve fizikçi James Franck (Nobel ödüllü) Türkiye'ye gelir. Üçü de Göttingen Üniversitesi'nden arkadaştırlar ve ağır toplardırlar. Bunlardan Richard Courant İstanbul Üniversitesi'nde Uygulamalı Matematik Enstitüsü için bir rapor hazırlar ve raporun sonunda enstitünün, özellikle matematik ve fizikte, birkaç yılda Avrupa standartlarına getirmenin mümkün olmadığını söyler. Bunun üzerine Türk Hükümeti enstitünün başına dünyaca ünlü birinin getirilmesinde ısrar eder. Richard Courant, Berlin'deki Uygulamalı Matematik Enstitüsü yöneticisi 50 yaşındaki Richard von Mises'i teklif eder. Von Mises, 1933-1939'da burada görev yapar ve 1943'te evleneceği Berlin'deki asistanı Hilda Geiringer'in de 1934-1939'da burada görev yapmasına neden olur. 1940'ta Almanya'dan gelenlerin ayrılması üzerine yerlerine genç elemanlar gelir. Örneğin, 1941'te Geometri Kürsüsü'ne Patrick Du Val gelir ve 1949'a kadar görev yapar. Cebirsel bir yüzeyin "Du Val tekilliği" kavramı ondan sonra adlandırılır. Aynı şekilde, Cahit Arf, Helmut Hasse'den ayrılıp İstanbul'a döndükten sonra kuadratik formlara çalıştı ve "Arf Halkaları, Arf Kapanışı, Arf İnvaryantı" adıyla anılan yeni keşiflerde bulundu. Yani İstanbul Üniversitesi Matematik Bölümü'ndeki kıpırdanmalar tam da Almanlar'ın ayrılmasıyla birlikte başladı (Bkz. "İstanbul Üniversitesi Fen Fakültesi Matematik Bölümü Tarihçesi").
Werner Romberg geliyor!
Werner Romberg (1909-2003) ülkemize gelmiş değil; çünkü onun hikayesi farklı. Romberg 1933'te Nazi zulmü nedeniyle Münih'ten Dnipro'ya kaçar. Fakat Hitler, 12 Mart 1938'te Avusturya'yı ilhak edince dikkatini şimdiki Çekya'ya yöneltir, dolayısıyla Mayıs 1938'de Oslo'daki arkadaşı Hylleraas'a yardım edebilmek için Varşova'dan Prag'a geçer. Ancak Hitler'in Münih Antlaşması nedeniyle burayı da işgal edeceğini anlayınca 20 Kasım 1938'te de Prag'tan Oslo'ya uçar. Hitler'in durmaya niyeti yoktur. Nitekim Weserübung Operasyonu 9 Nisan 1940'ta devreye sokulunca Oslo da saldırılardan nasibini alır ve bu yüzden Oslo'dan Upsala'ya kaçar. 1940-1944 arası burada kalır ve 1944'te Oslo özgürlüğüne kavuşunca geri döner. Burada Hylleraas'ın asistanı olarak resmi bir pozisyon alır ve 1947'de Norveç vatandaşı olur.
Daha sonra Norveç Bilim ve Teknoloji Enstitüsü Tröndheim'da olduğundan buraya yerleşir ve orada kuzey ışıkları altında Nümerik İntegral'deki o ünlüyü katkıyı yapar. DKNVS, bu ünlü katkıyı yazar. 14 Şubat 1955'te yapılan toplantıda sunum görevi NTH'deki (ki şimdi NTNU) Matematik Bölümü Başkanı Prof. Dr. Sigmund Selberg'e verilir ve 28 Nisan 1955'te de Komisyon Başkanı F. Bruns Bokhandel'in onayıyla, "Vereinfachte numerische Integration (Basitleştirilmiş Nümerik İntegral), Norske Vid. Selsk. Forh. (Trondheim) 25 (1955) 30-36" adıyla tüm dünyaya duyurulur.
Şimdi Romberg'in bu tezine takla attıran çalışmayı aşağıdaki dosyamda bulabilirsiniz. Bakın bakalım, Romberg Türkiye'ye gelmiş mi?
Romberg İntegrali Kronolojim 3:
Bölüm 1: Trapez Metodu'nun Geometrik Yorumu ve Sonuçları, S. 1-19.
Bölüm 2: Romberg Metodu'ndaki Algoritmalar İçin Ekstrapolasyonlar, S. 20-33.
Bölüm 3: Matematik Programları ve Demoları, S. 34-39.
Bölüm 4: Ekler, S. 40-58.
Not: Dosya boyutu 29081 KB olduğundan Microsoft Edge açmaya çalışırken çöker. Yani büyük boyutlu PDF dosyalarında Microsoft Edge'te çökmeler yaşanıyor. Buna göre büyük boyutlu PDF dosyalarını gözatıcıda okurken Chrome ve Microsoft Explorer'ın kullanılmasını tavsiye ederim!
Ben size ne demiştim; Romberg'i Türkiye'ye getireceğim. Çünkü 2016'dan bu yana biricik amacım bu idi!
GÜNCELLEME
11.02.2020, 11:00.
Bu kronolojik çalışmamı 21 Ocak 2020'de yayımlamıştım, ama Werner Romberg'in 5 Şubat 2020'de 17. Ölüm Yıldönümü sözkonusu olunca bu sefer daha yetkin bir çalışma içine girmek zorunda kaldım.
 Solda Romberg (Aralık 1988) ve sağda ben (İstanbul Arkeoloji Müzesi, M.Ö. 1-M.S. 1. yy. Roma Heykelleri Bölümü, 23.10.2004, 15:10). Yani bu görüntüm, Romberg İntegrali Kronolojim 3'te sözüne ettiğim E-ATA 1 Algoritmaları'nı yazdıktan, özellikle Tablo 2.4'te geçen tarihten 2 yıl sonraki halimdir. Posseidon'un ayıplı bölgesini RTÜK gereği kapattım.
Solda Romberg (Aralık 1988) ve sağda ben (İstanbul Arkeoloji Müzesi, M.Ö. 1-M.S. 1. yy. Roma Heykelleri Bölümü, 23.10.2004, 15:10). Yani bu görüntüm, Romberg İntegrali Kronolojim 3'te sözüne ettiğim E-ATA 1 Algoritmaları'nı yazdıktan, özellikle Tablo 2.4'te geçen tarihten 2 yıl sonraki halimdir. Posseidon'un ayıplı bölgesini RTÜK gereği kapattım.Güncellemeye sadece "1.7.3 Romberg'in Örnekleri"ni ekledim ve bir Önsöz yazdım. Bunun dışında, Romberg İntegrali Kronolojim 3 adlı PDF dosyam güvenlik nedeniyle tüm işlemlere kapalıdır; sadece yüksek çözünürlüklü yazdırma işlemini yapabilirsiniz.
BAKIN BURASI ÇOK ÖNEMLİ!!!
Dosyanın kapak boyutu 18.9 MB ve onu dosyayla birleştirdiğim zaman 28.6 MB oldu. Fakat bu dosyada ilk 2 kronolojide olduğu gibi orijinal ve orijinal olmayan bölümleri vurgulamak için MS Word'te aktif ve pasif işlemlerini yaptığım boyut 59.2 MB oldu. Bu nedenle dosyayı siteye ilk koyduğumda bazı gözatıcıların (MS Edge vb.) açamadığını ve sonrasında da dosyaya hiçbir gözatıcıyla ulaşamadığımı (okuma ve indirme) gördüm. İşte bu tür durumlarda dosyaya hızlıca ulaşabilmek için bir VPN kullanmanız gerekir!
Rakamlarla RİK3.pdf: Bilgisayarımda bu dosya için RİK 3 adlı klasörün içinde 6 klasör, 87 dosya ve bunların boyutlarının toplamı olan 522 MB için bizzat çalışmalarda bulunduğumu biliyor musunuz? Harcanan süreyi söylemiyorum bile!




