Yurtdışındaki üniversitelerde olduğu gibi bizim üniversitelerde de top örnek olarak kabul edilen (bkz. "Chapter 07.04 Romberg Rule of Integration"),
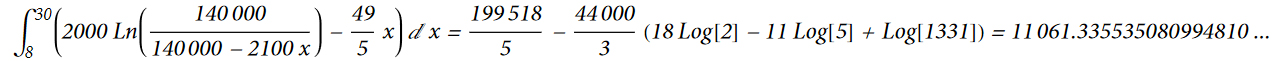
integraline ve değişken dönüşümle elde edilen
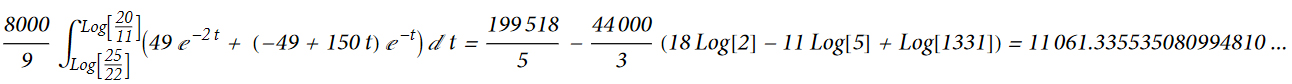
diğer şekli (ki bunu yakınsaklığı artırmak için yapmıştım) olmak üzere 2 farklı şekline genel haldeki Ole Amble'ın algoritmik çiftine 2. tür E-ATA Algoritması'nı uyguladım. İkincisinden çıkan sonuçlar daha iyiydi (Bkz. "2. Tür E-ATA M Algoritması Üzerindeki Genel Haldeki Ole Amble Algoritması'na Mathematica İle Sembolik Bir Yaklaşım").
Bu şekilde integral hesaplarını Ole Amble (1952-1996) ve Werner Romberg (1955-2003) zamanında yapmak mümkün değildi. Çünkü kullandığım ekstrapolasyonu Romberg öldükten (5.2.2003) hemen sonra (14.5.2003) keşfetmiştim. Ama bu ekstrapolasyonun farkına varmam 2018 yazında gerçekleşmişti. Çünkü düzgün çokgenlerle hesaplanan pi sayısı için yazdığım bu ekstrapolasyonu unutmuştum! Bu durum 2018 yazında lineer ekstrapolasyonları tekrar keşfettikten sonra "ATA Algoritmaları, 2003"na döndüğümde ortaya çıkmıştı. Yani bu ekstrapolasyonu 2. kez keşfediyordum! 2018'deki keşif 2003'tekine göre daha da genel haldeydi ve bu son şekliydi. Çünkü bu ekstrapolasyonu 2018'dekine göre daha da genelleştirmek ya da en karmaşık şekilde yazabilmek mümkün değildir!

